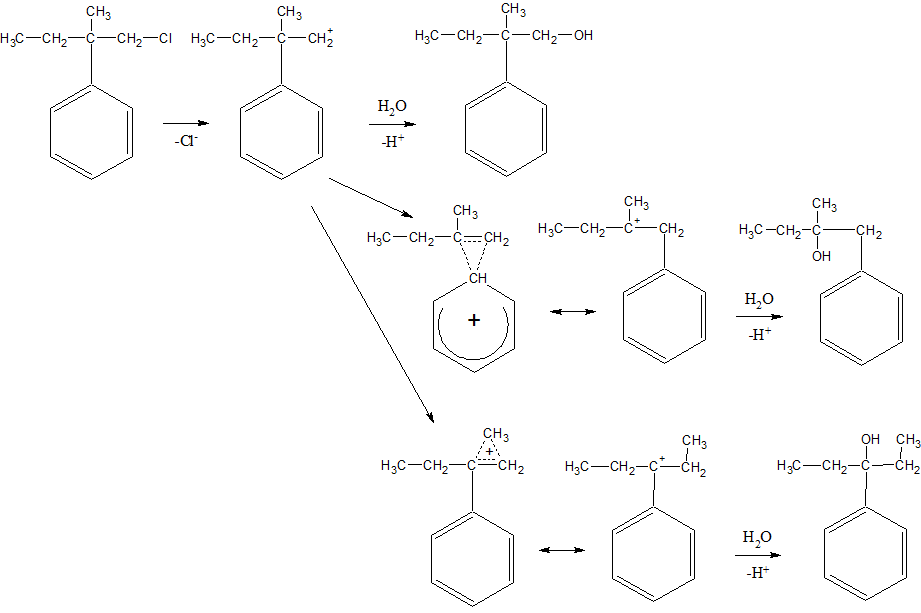-
Постов
34959 -
Зарегистрирован
-
Победитель дней
1166
Весь контент yatcheh
-
Ну, это частный случай. Надо стремиться объять необъятное...
-
Нуклеофильное замещение. Атом азота пиридина, благодаря своёй неподелённой электронной паре - нуклеофил, а атом углерода в катионе триметилсульфония - электрофил. Пиридин замещает серу у атома углерода: C5H5N + CH3-S+(CH3)2 => [C5H5N.....>CH3....>S(CH3)2]+=> C5H5N+-CH3 + S(CH3)2 Получается хлорид N-метилпиридиния и диметилсульфид
-
Вот это вопрос концептуальный. Мне он не пришёл в голову, а зря. Фенил - это ведь π-донор, а карбоксил и сульфонил - акцепторы. Если прикинуть механизмы: То для трихлорметилбензола и бис(трихлорметилкарбоната) всё выглядит замечательно - так или иначе, по Sn1 или по Sn2 (в случае карбоната, где возможна прямая атака на карбонил), в реакции с ацетатом всё скатывается к хлорангидридам, ну и дальше - сами понимаете. А вот для гексахлордиметилсульфона не всё так просто. Sn1 тут - невероятен, для Sn2 - серьёзные стерические препятствия, хотя, если они преодолимы, то реакция может пойти, но более затейливо, в продуктах и полупродуктах можно помыслить и фосген, и СО, и тионилхлорид, и SO2, и ещё бог знает что... Или она просто не пойдёт, а гексахлордиметилсульфон окажется такой же беспонтовой шнягой, как и друзья его - диметилсульфон и сульфурилхлорид Вот если бы это был бис(трихлорметил)сульфат - другой разговор!
-
ChemSketch фриварный
- 3 ответа
-
- 1
-

-
Более нуклеофильный. Видимо - м-нитрофенол. Хлорангидрид.
-
Нет, ангидридов там не будет. Это было бы слишком вкусно Нарисовать можно, но будет ли... Я думаю не будет, но то - такое...
-
Поскольку реакционный центр в этом соединении стерически весьма загружен, реализация механизма SN2 будет затруднена. Механизм же SN1 включает образование первичного карбкатиона (с отщеплением аниона Cl-). При реакции этого карбкатиона с водой образуется нормальный продукт гидролиза. Но рядом с катионным центром имеется фенильный радикал с подвижной пи-системой, который может образовать с катионным центром циклический переходный комплекс, перегруппировывающийся с переносом фенильной группы и образованием более устойчивого третичного карбкатиона. Реакция этого карбкатиона с водой приведёт к "аномальному" продукту замещения. Другой вариант - перенос метильной группы с образованием ещё более стабильного третично-бензильного катиона. Но в этом случае скорость реакции будет ограничиваться более высокой энергией переходного состояния, и этот продукт будет минорным (утверждение напрашивается, но мне оно кажется несколько притянутым за уши).
-
Ога. Можно чё-нить отформилировать. 1,4-Диметоксибензол, например
-
Трихлорметил -CCl3 даже в виде трихлорметилбензола - хлорирующий агент. Хлорирующий в том смысле, что легко меняет хлор на кислород. Хлорирует кислоты и оксиды. C6H5-CCl3 + R-COOH => C6H5-COCl + R-COCl + HCl 3C6H5-CCl3 + Fe2O3 => 3C6H5-COCl + FeCl3 2C6H5-CCl3 + SO3 => 2C6H5-COCl + SO2Cl2 Реакция CCl4 с олеумом - из той же серии. Так что следует ожидать подобного поведения: SO2(CCl3)2 + H2SO4 => 2SO2Cl2 + 2HCl + 2CO SO2(CCl3)2 + 2SO3 => 3SO2Cl2 + 2CO
-
Не успевает. Но вообше - это препаративная реакция. Получается CH3-C(=NH)-O-OH, которая быстро разлагается с отщеплением кислорода. Единственный рабочий способ частичного гидролиза нитрилов до амидов.
-
CH3CN + H2O2(30%) => CH3-CONH2 + H2O + O2 Выход почти количественный, при н.у., главное - не взорваться от избытка кислорода
-
Вторая - ацилирование. А вот первую назвать алкилированием было бы не корректно, ведь вводится не алкильная группа, а алкенильная. Тогда уж - "алкенилирование", в литературе встречается. Хотя нет, тоже ерунда. Алкенил - это не то, это просто непредельный радикал. "Алкенилиденирование" - во! "Винилиденирование" же есть, почему не быть более общему термину?
-
Ацетамид получают нагреванием хлористого аммония с ацетатом натрия до 240С (СОП 1, 63 - примечания).
-
Он плохо в нём растворяется. Автоклав нужен И соль аммония в качестве катализатора.
-
Поверхность контакта фаз - немаловажное обстоятельство, кто ж спорит. Но и от термодинамики никуда не убежишь. Конкретно в случае этилацетата и водного аммиака, у ЭА изрядная растворимость в водном слое, и как раз тут интенсивность перемешивания мало влияет на скорость. Достаточно, что бы перемешивание просто - было. Этилхлорацетат с водным аммиаком реагирует в сотни раз быстрее - приходится охлаждать смесь льдом, иначе закипеть может. При этом с водой он так же не смешивается. Так что всё зависит от конкретных веществ и вещей. Получится равновесная смесь, никак не 100% Будут болтаться аммиак, этилацетат, ацетамид, спирт, вода, ацетат аммония. Если долго упираться рогом, то останется только ацетат аммония, спирт, вода, и избыток аммиака. Вот если бы аммиак был не водный...
-
Ускорить можно только нагреванием в автоклаве под давлением аммиака. Можно смесь ацетата аммония с уксусной перегнать (СОП 1, 63). 90% выход.
-
В 92-м году пил как-то я спирт с явным запахом эфира. По мозгам бьёт как кувалдой. Жаль, что не по ногам. Очухался на другом конце города в промзоне, без косухи, без сумки, но в курсантской шинели и с сапёрной лопаткой. До сих пор интересно - а шо в промежутке-то было?
-
Можно с любой. Но не нужно. Проще сначала обычной перегонкой сконцентрировать до 50%-70% (у самогонщиков это отлично получается), а потом уже другие методы использовать. Мне на самодельной колонке с головкой полной конденсации удалось вытащить практически весь спирт в 95% виде из ведра 0.5% водного раствора в один приём. Не то, что чекушки водки было жалко, вылитой в ведро, а чисто шоб позырить - как это работает Вместо ГПК можно поставить ту же насадку Дина-Старка. А в качестве насадки для колонки - китайскую кухонную губку с базара. Это не важно. Если есть колонка/дефлегматор - это совершенно неважно.
-
Бо'льшая часть спирта уходит в слой циклогексана, и возвращается в оборот.
-
Я имел в виду ОВ раздражающего действия Cl-CH=N-OH "монохлорформоксим". Или его более стойкого собрата - Cl2C=N-OH. 2CH2NCl + H2O => ClCH=NOH + [CH2=NH]*HCl Для лакримирующего действия его нужно совсем немного.
- 51 ответ
-
- 1
-

-
Да ещё Эйнштейн этим вопросом заморочился. В результате в ОТО гравитация - это не поле, не потенциальное поле. Это свойство пространства. И остались в качестве гарантов силы одни ускорения. "Ускорение силы тяжести" - из той же оперы. Силы нет, есть ускорение. И сила - всего лишь терм в математическом выражении.